How to Count Numbers

最初に一言

ここに書いている内容は最近、出版されているC言語の一般的な本には書かれていない内容である。「じゃあ、必要ないからとばそー。」いいよ、もちろん飛ばしてくれても。

ここで書いてある内容はC言語というよりも、プログラミングをやる人間としての常識が書いてある。この程度のことは誰でも知っているということだ。

まあ、ここはプログラミング初心者がターゲットなので書いてみた。正直にいうとここの内容を知らなくてもC言語は組める、今となっては。ただ・・・

プログラマーとしてなめられたくない。
情報処理技術者試験 (http://www.jitec.jp/") の基本情報処理技術者の資格を取るなら必須。

ということなので知っていて損するはなしではないと思う。

「普通」な数の数え方

我々はどうやって物の個数を数えているのだろうか。ちょっとおさらいしよう。「そんなの小学一年生のときにおはじきを使って習ったよ。」という人も辛抱して付き合ってほしい。

ここでは例として「●」の個数を数えることにしよう。

_: 何もない、つまり0個。
●: 1個。
●●: 2個。
●●●: 3個。
●●●●: 4個。
●●●●●: 5個。
●●●●●●: 6個。
●●●●●●●: 7個。
●●●●●●●●: 8個。
●●●●●●●●●: 9個。
●●●●●●●●●●: ここでなんと桁が一つ増える。10個。
●●●●●●●●●●●: 11個。
●●●●●●●●●●●●: 12個。
●●●●●●●●●●●●●: 13個。
●●●●●●●●●●●●●●: 14個。
●●●●●●●●●●●●●●●: 15個。
●●●●●●●●●●●●●●●●: 16個。

・・・と続いていくわけである。

「バカ野郎、それぐらい知っているわい、ボケ!」という言葉が聞こえてきそうなので、ちょちょっとまとめておこう。

我々の数字の数え方は"0, 1, 2, 3, 4, 5, 6, 7, 8, 9"の計10個の記号を使って示されている。そして一つ下の桁でこれら10個の記号を使い切ると桁が一つ増え、元の桁は"0"になる。

このように10個の記号を使った数字の表現方法を10進数というんだ。僕らは日々、使っている数字のことだよ。

「じゃあ、そうじゃない数え方ってあるの?」あるんだな、これが。コンピューターの世界じゃ2進数とか16進数がよく使われるんだ。

"0, 1"の世界

コンピューターの世界では2進数ってのがよく使われる。もう想像はつくと思うけど"0, 1"という2個の記号を使って数を表現することだ。

よく「コンピューターは"0, 1"の世界」だとかいわれるけど、そのことだね。だた、これって不思議な表現だよなあ。じゃあ、「コンピューターでは"2"は表現できないのか」ということになりそうだな。そんなこたーない。ためしに2進数で「●」の数を数えてみよう。

_: 何もない、つまり0個。
●: 1個。
●●: 2個。

じゃないんだな。"2"っていうのは2進数の世界には存在しない記号なんだ。既に"0, 1"の記号を使い切っているわけだから桁を増やして

●●: 10個。

「でも2個しかないのに10個?」それは恐らく読み方を間違っているからだよ。10進数じゃないんだから"10"は「じゅう」ではなく、「いちぜろ」と読むべきなんだ。まあ、続けてみるよ。

●●●: 11個。
●●●●: 12個。

だから"2"はないって。くりあがりくりあがり・・・

●●●●: 20個。

だから"2"はないって言っているだろう、ボケ!・・・失礼しました。桁を増やして・・・

●●●●: 100個。

となります、はい。もう面倒だからいちいち書かないけどこれの繰り返しだ。

●●●●●: 101個。
●●●●●●: 110個。
●●●●●●●: 111個。
●●●●●●●●: 1000個。
●●●●●●●●●: 1001個。
●●●●●●●●●●: 1010個。
●●●●●●●●●●●: 1011個。
●●●●●●●●●●●●: 1100個。
●●●●●●●●●●●●●: 1101個。
●●●●●●●●●●●●●●: 1110個。
●●●●●●●●●●●●●●●: 1111個。
●●●●●●●●●●●●●●●●: 10000個。

しかしこれ、一見しただけでは2進数か10進数かわからないよな。だから普通は右下に2進数を意味する小さな2を括弧書きでつける。例えば1011₍₂₎=11見たいな感じ。

ちなみに10進数のときは1の位のことを「1桁目」、10の位のことを「2桁目」とかいうけど2進数の場合はどうなるのだろうか。

まず、10進数における「1の位」とか「10の位」という表現方法の2進数バージョンは存在しないといった方がいいだろう。一応、桁の上がり方を考えると「1の位」、「2の位」、「4の位」という言い方ができないわけではないが滅多に聞かない。

ただ、「2進数における桁」のことをビット(bit)という。2進数における一番右のケタが「0ビット」(1ビットではないことに注意)、そして左の桁にいくにつれて「1ビット」「2ビット」という。例えば110₍₂₎において「0ビット」は"0"、「1ビット」は"1"、「2ビット」は"1"である。

また、ビットにはその2進数の桁数、という意味も同時にもっている。例えば110₂は3ビットである。さらにハードディスクの容量などを示すのによく用いられるバイト(byte)という言い方もあるがこれは8ビットのことである。つまり、鉛筆12本が1ダースなのと同じような感じである。この表現方法もよく使われ、「日本語の1文字を表示するのには2バイト(=16ビット)必要である。」という使い方をするわけだ。

2進数←→10進数

結局のところ、10進数と2進数なんて表記方法が違うだけってことがわかったと思うが「10進数と2進数ってどうやって変換するの?」という疑問があるんじゃないかしら。上では頑張って「●」を書いたが毎回、そんな面倒なことをやる必要はない。計算する方法がちゃんとある。

2進数→10進数

まあ、込み入った話をすると切がないので完結にいこう。多分、細かいところは、やり方がわかればわかると思う。

0ビットが"1"とは10進数で"1"を示し、1ビットが"1"は10進数で"2"を示す。以後、同様に2ビットが"1"は10進の"4"、3ビットが"1"は10進の"8"、4ビットが"1"は10進の"16"である。ここまではすでにわかっていただけているはず。混乱したら●を数えてみるべし。

何が言いたいのかというと、nビットが"1"は10進数で"2のn乗"ということになる。つまり2ⁿである。とどのつまり、2をn回、掛けるのである。ちなみに2⁰=1である。

だから、図のように計算すればよい。

要点は各ビットで"1"の部分に対応する10進数を足せばいいわけだ。簡単だろう?

10進数→2進数

これはちょっと難しい。いや、やり方は覚えてしまえば大したことないんだけど理屈を説明しだすと長くなる。というわけで説明しない。やり方だけ書いておく。まあ、じっくり考えればわかることなんだけどね。

取りあえず、変換したい数を2で割る。答え(商)をさらに2で割っていく。最終的に答え(商)が0になるまで繰り返すわけだ。このとき、割り算の過程で出てきた余りを右から並べたものが2進化された数字である。

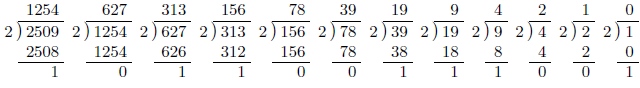
あまりを右から左に読んでごらん。

四則演算

では、足し算引き算掛け算割り算はどうやってやるのよ?

2進数を10進数に変換、計算、また2進数に戻すという方法なら既に出来るだろう。しかしばかばかしい。そんな面倒なこと、やってられん。そういうわけで直接、2進数で四則演算をやろう。

その前にはっきり断っておこう。C言語を組むにあたって2進数の四則演算の仕方を知っておく必要はない。ま、教養ってことだ。あ、アセンブラを使うのなら必須だけど。

やり方は基本的には10進数と同じなので・・・みればわかると思う(爆)。注意点は繰り上がり、繰り下がりの部分。1₍₂₎+1₍₂₎=10₍₂₎、10₍₂₎-1₍₂₎=1₍₂₎。

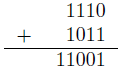
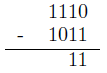
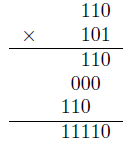
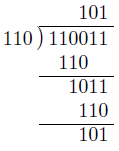
負の数

ではプレスの数、マイナスの数はどうするのよ?

「そんなの簡単だよ、横棒をつければいいだけでしょ。例えば-1011₍₂₎みたいに。

あまりそういう表現方法って聞いたことがないなあ。実は2進数にはこういう横棒を付けずに負の数を表現できるんだ。

1の補数表現

例えば「6の正負をひっくり返した-6はどうなるのよ」6 = 0110₍₂₎の負の数は次のようにすれば求められるのだ。その前に今は4ビットであると限定しておこう。いや、何ビットで限定してもいいんだけどとりあえず、ね。

それは各ビットを見て、"1"だったら"0"に、"0"だったら"1"にする。これだけ。「えっ!」っと思うなかれ、実際にやってみよう。

例えば6 = 0110₍₂₎の場合は各ビットを反転させるわけだから-6 = 1001₍₂₎となるわけだ。これだけ。

「え、1001₍₂₎って9じゃないの?」その通りだ、正の数だけを考えているのなら。ただ、今は負の数を考えているよと前置きしたでしょ。で、前に4ビットであると限定するっていったでしょう。このとき実際、正の数として考えるのは下位の3ビットだけなんだ。上位1ビットは負の数を表現するために使われてしまっているので使えないのだ。そういうわけでこの例のように4ビットにした場合、表現できるのは0111₍₂₎の7までということになるのだ。逆に負の数も1000₍₂₎で-7までとなる。最初に述べた「今は4ビットであると限定しておこう。」とはそういう意味だ。

「で、横棒つけて-110₍₂₎と書いただけと比べて何がありがたいのよ。」それは四則演算が矛盾なくできるのだ。中学校で習った知識を思い出してほしい。6 - 6 = 0である。で、これは6 + (-6) = 0と同じである。そう、引き算は引かれる数を負の数にして足し算するのと同じことだ。で、これが2進数ですんなりといけるのだ。ためしてみるとこうなる。

110₍₂₎ + 1001₍₂₎ = 1111₍₂₎

ところで-0 = 0だから0000₍₂₎ = 1111₍₂₎ = 0なのでたしかに6 + (-6) = 0が確認できた。便利だ。

こうやって単純に各ビットを反転させて負の数を表現する方法を1の補数表現というのだ。ただ、上で述べたようにこの方法、0を表現する方法が二通りもある。なので普通はあまり使われなかったりする。よくつかわれるのは次のやつだ。

2の補数表現

そういうわけでもう一つの方法だ。2の補数表現はこうやる。

それは各ビットを見て、"1"だったら"0"に、"0"だったら"1"にする。そして"1"を足す。これだけ。「えっ!、1の補数表現に1たしただけ?」まさにその通りだ。

実際にさっきの6 + (-6) = 0をやってみよう。こうなる。

0110₍₂₎ + 1010₍₂₎ = 10000₍₂₎

ところで、今は4ビットで考えているので5ビットになった場合、最上位ビットは捨てる。だから結果は0000₍₂₎ = 0である。めでたしめでたし。

2の補数表現を使うと1の補数表現にあった「0が二通りある」といったことがなくなる。「でもさあ、最上位のビットを捨てるって作業が増えたよ。」実は考えている以上のビットを捨てるという作業はコンピュータに取っては作業ではない。というより、「失われる」に近い。コップに水を入れすぎた状態なのだ。つまり、絶対あふれるわけだ。なので別に手間が増えているわけではないのだ。実際、コンピュータの内部では通常、こうやって負の数が表現されているわけだ。

ちなみに4ビットの場合、1の補数表現だと-7から+7までだったが2の補数表現だと-8から+7までとなる。1000₍₂₎ = -8だ。

少数

もう面倒だしC言語に必要ないし、疲れたので概要だけ書いておく。実はこれも二通りの表現方法がある。

固定小数

固定少数っていうのは小数点の位置が決まっているということだ。後から出てくる浮動少数と比べてもらえばわかると思う。

各ビットをnとした場合、そのビットは2ⁿだ。だから2ビットは"4"の位、1ビットは"2"の位、0ビットは"1"の位、では0ビットより1つ右は"1 / 2 = 0.5"の位、2つ右のは"1 / 4 = 0.25"の位、3つ右は"1 / 8 = 0.125"の位となる。どうやって10進数から変換するかは・・・考えればわかるかもしれないけどいいや、どうだって(爆)。

何故なら「実はコンピュータで固定少数は使わない」。

・・・なんだけど実は以下の浮動小数の中で使われていたりして。

浮動少数

浮動少数っていうのはつまり3.141592 * 10³みたいな書き方のことだ。実際にはこの例だと3.141592と3(それぞれ仮数部、指数部っていう)をもって表現することだ。こうすると指数部を変えればどんなに少数以下が深い少数も表現できるでしょう。つまり、小数点を指定する部分と実際の値が独立しているので浮動少数っていうんだ。ただ、それだけ。コンピュータでは浮動少数が一般に使われる。もちろん、仮数部、指数部それぞれ内部的には2進数で扱われているけどね。で、仮数部には実は固定小数が使われていたりする。意識することはあんまりないけど実はこれに関する罠もあるけど、今は省略。

16進数

ところで、すでに気が付いていると思うけど2進数って使いにくい。何故かというと・・・

桁が多くなる。100=1100100₍₂₎である。
通常は10進数を使うにしても2進数と10進数の変換は面倒。

そこれで16進数の出番で実際には2進数よりもよく使われる。まあ、何故、よく使われるかはおいておくとして、16進数とは何か、からだ。

もう、わかっていると思うが16進数とは16個の記号を使って数を表現する方法だ。

「え?そんな、われわれは"0, 1, 2, 3, 4, 5, 6, 7, 8, 9"の計10個の数字しか使ってないよ。2進数のときは"0, 1"を使ったけど今回はどうするの?」

うーん、困った。というわけで通常は"0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F"の16種類の記号を使うんだ。つまり、足りない分はアルファベットを割り当てたわけだね。ちなみにアルファベットは大文字でも小文字でも構わない。

実際の数え方は・・・もう、面倒だ。だから書かない。けど表にまとめておく。2進数、16進数、10進数の変換表だ。

10進数	2進数	16進数
0	0	0
1	1	1
2	10	2
3	11	3
4	100	4
5	101	5
6	110	6
7	111	7
8	1000	8
9	1001	9
10	1010	A
11	1011	B
12	1100	C
13	1101	D
14	1110	E
15	1111	F
16	10000	10

ちなみに16進数は最後にHを付けて書くことが多い。16=10Hだ。

で、この表をよく見て欲しい。何故、16進数がよく使われるかがわかる。2進数から16進数への変換(逆も)が楽だからだ。

「えー、大変そうだよ～」ヒントは最後の10000₍₂₎=10Hのところ。そう、16進数が桁上がりするとき、同時に2進数も桁が上がっているのだ。

ということは例えば101110001₍₂₎を16進数で書くとどうなるか。見やすくするために4ビット毎にカンマで区切ってみるとこうなる。

1,0111,0001₍₂₎=1,0000,0000₍₂₎+111,0000₍₂₎+1₍₂₎

だからこうなる。

1,0111,0001₍₂₎=100H+70H+1H=171H

つまり、1011100001₍₂₎=171Hなのだ。そう、上にある表さえ抑えておけば楽勝なのだ。つまり2進数と16進数の変換は2進数を4桁ごとに区切ってそれぞれを表にしたがって変換すればいいだけなのだ。逆もしかりだ。

アセンブラをやる人間だったら上の表はもはや「常識中の常識」なのだ。Cプログラマーにそれが必要なのかは知らない。が、僕は今でもこれはプログラマーとしての常識だと確信しており、例えば「1A8FHは2進数ではいくら?」というのを上の表を見ずに変換できない奴の組んだプログラムを信用するのは怖い。やっぱり常識だ。ちなみに1A8FH=1110010001111₍₂₎。